이분 탐색
BigO: O(log N)
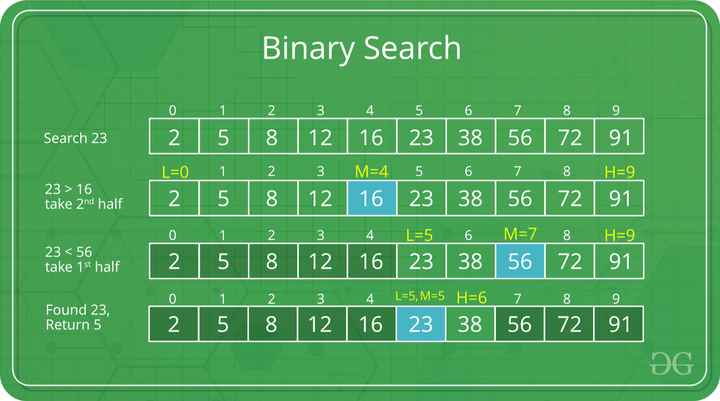
결정 문제의 답이 이분적일 때(Yes or No) 사용할 수 있는 탐색 기법이다. 데이터가 오름차순 정렬된 배열에서 특정 값(N)을 찾아낸다. 정렬된 리스트에서 검색 범위를 줄여 나가면서 검색 값을 찾는다. 검색이 반복될 때마다 검색 범위가 반으로 줄어들기 때문에 속도가 빠르다.
예를 들어서 1~50의 숫자가 오름차순 정렬된 카드 더미에서 28번 카드를 찾는다고 가정하자. 첫 번째 카드부터 I번째 카드는 v[i], 28은 val로 정의할 때, 우리가 찾고자 하는 값은 i를 증가시키면서 v[i] >= val가 되는 지점(처음 결정 문제가 True가 되는 지점)의 i 값이다.
이분 탐색의 아이디어는 경계를 포함하는 구간 [start, end]을 잡은 뒤 구간의 길이를 절반씩 줄여나가며 start와 end가 경계 지점에 위치하도록 하는 것이다. 이분 탐색이 끝난 뒤엔 start의 다음 칸은 end(start + 1 == end)이며, Check(start) != Check(end)이다. 이때 Check(x)는 결정 문제의 파라미터가 x일 때 결정 문제의 답을 의미한다. 위의 예시에서는 [27, 28]로 start와 end를 줄여 나간 뒤 end = 28을 찾으면 된다.
구현은 Check(start) != Check(end)가 되도록 초기값을 잘 설정해 준 뒤 start + 1 < end인 동안 mid = (start + end) / 2를 구해서 Check(start) == Check(mid)라면 start = mid를, Check(end) == Check(mid)라면 end = mid를 해 준다. mid는 항상 start < mid < end를 만족한다. 따라서 구간의 길이는 매번 절반씩 줄어들며 언젠가는 start + 1 == end가 되어 반복문을 탈출한다.
만약 결정 문제의 답의 분포가 A ~ B일 때, 정답이 가장 큰 A라면 start를, 가장 작은 B라면 end를 출력한다.
- 경계를 포함하도록 start와 end를 잡는다.
- 리스트의 중간 값을 정의한다.
- 중간 값(mid)과 검색 값(target)을 비교한다.
- mid = target: 종료
- mid < target: 중간 값을 기준으로 리스트의 오른쪽 구간을 탐색한다.
- mid > target: 중간 값을 기준으로 리스트의 왼쪽 구간을 탐색한다.
- 값을 찾거나 리스트에 해당 값이 존재하지 않는 경우를 찾을 때까지 반복한다.
def binary_search(target, data):
data.sort()
start = 0
end = len(data) - 1
while start <= end:
mid = (start + end) // 2
if data[mid] == target:
return mid
elif data[mid] < target:
start = mid + 1
else:
end = mid - 1
2470번: 두 용액
🥦 문제
KOI 부설 과학연구소에서는 많은 종류의 산성 용액과 알칼리성 용액을 보유하고 있다. 각 용액에는 그 용액의 특성을 나타내는 하나의 정수가 주어져있다. 산성 용액의 특성값은 1부터 1,000,000,000까지의 양의 정수로 나타내고, 알칼리성 용액의 특성값은 -1부터 -1,000,000,000까지의 음의 정수로 나타낸다.
같은 양의 두 용액을 혼합한 용액의 특성값은 혼합에 사용된 각 용액의 특성값의 합으로 정의한다. 이 연구소에서는 같은 양의 두 용액을 혼합하여 특성값이 0에 가장 가까운 용액을 만들려고 한다.
예를 들어, 주어진 용액들의 특성값이 [-2, 4, -99, -1, 98]인 경우에는 특성값이 -99인 용액과 특성값이 98인 용액을 혼합하면 특성값이 -1인 용액을 만들 수 있고, 이 용액이 특성값이 0에 가장 가까운 용액이다. 참고로, 두 종류의 알칼리성 용액만으로나 혹은 두 종류의 산성 용액만으로 특성값이 0에 가장 가까운 혼합 용액을 만드는 경우도 존재할 수 있다.
산성 용액과 알칼리성 용액의 특성값이 주어졌을 때, 이 중 두 개의 서로 다른 용액을 혼합하여 특성값이 0에 가장 가까운 용액을 만들어내는 두 용액을 찾는 프로그램을 작성하시오.
🥦 분석
반복문을 통해 리스트의 각 용액들을 기준으로 하여 나머지 용액과 더했을 때 0과 가까운 용액을 찾는다. 예를 들어서 A, B, C, D, E 용액이 있을 때, 첫 번째 반복문을 A 용액을 기준으로 하고 B, C, D, E를 하나씩 더했을 때(이때 이분 탐색을 적용한다.) 0에 가까운 용액을 찾는다.
- 현재 용액의 오른쪽에 있는 용액부터 마지막 용액까지의 중간값(인덱스)을 변수 mid로 정의한다.
- 현재 용액과 중간 값(mid)을 인덱스로 하는 용액을 더한 값이 0과 가장 가까운 값인지 판별한다.
현재 mid을 통해 만든 비교할 값(s) = target일 때는 이 문제의 경우 갱신이 필요하지 않다.
0과 가까운 수를 저장해 둔 min_s의 값과 비교해서 현재의 값이 더 0에 가까우면 갱신하고, v1과 v2에 각 용액의 값을 갱신한다.
- 현재 mid을 통해 만든 비교할 값(s) < target: 중간 값을 기준으로 리스트의 오른쪽 구간을 탐색한다.
- 현재 mid을 통해 만든 비교할 값(s) > target: 중간 값을 기준으로 리스트의 왼쪽 구간을 탐색한다.
- 반복이 끝나면 저장해 둔 v1과 v2의 값을 출력한다.
🥦 풀이
n = int(input()) # 전체 용액의 수
arr = sorted(list(map(int, input().split()))) # 각 용액의 특성값
min_s = 2000000001 # 두 용액의 합 (0과 가까워야 한다)
if n == 2:
print(arr[0], arr[1])
exit(0)
for i in range(n - 1):
start = i + 1 # 현재 값의 오른쪽 값부터 탐색
end = n - 1 # 인덱스 주의
while start <= end:
mid = (start + end) // 2
s = arr[i] + arr[mid] # 두 용액의 합
if abs(s) < min_s: # 두 용액의 합이 0과 더 가까운 값이라면 갱신
v1, v2 = i, mid
min_s = abs(s)
if s < 0: # 두 용액의 합이 0보다 작다면
start = mid + 1 # 오른쪽 구역 탐색
else:
end = mid - 1
print(arr[v1], arr[v2])
2473번: 세 용액
🌷 문제
KOI 부설 과학연구소에서는 많은 종류의 산성 용액과 알칼리성 용액을 보유하고 있다. 각 용액에는 그 용액의 특성을 나타내는 하나의 정수가 주어져있다. 산성 용액의 특성값은 1부터 1,000,000,000까지의 양의 정수로 나타내고, 알칼리성 용액의 특성값은 -1부터 -1,000,000,000까지의 음의 정수로 나타낸다.
같은 양의 세 가지 용액을 혼합한 용액의 특성값은 혼합에 사용된 각 용액의 특성값의 합으로 정의한다. 이 연구소에서는 같은 양의 세 가지 용액을 혼합하여 특성값이 0에 가장 가까운 용액을 만들려고 한다.
예를 들어, 주어진 용액들의 특성값이 [-2, 6, -97, -6, 98]인 경우에는 특성값이 -97와 -2인 용액과 특성값이 98인 용액을 혼합하면 특성값이 -1인 용액을 만들 수 있고, 이 용액이 특성값이 0에 가장 가까운 용액이다. 참고로, 세 종류의 알칼리성 용액만으로나 혹은 세 종류의 산성 용액만으로 특성값이 0에 가장 가까운 혼합 용액을 만드는 경우도 존재할 수 있다.
산성 용액과 알칼리성 용액이 주어졌을 때, 이 중 같은 양의 세 개의 서로 다른 용액을 혼합하여 특성값이 0에 가장 가까운 용액을 만들어내는 세 용액을 찾는 프로그램을 작성하시오.
🌷 분석
- 0 ~ (용액의 수 - 2)까지의 수를 기준(반복문)으로 하고, start = (기준 값 + 1), end = (용액의 수 - 1)로 시작점을 잡는다.
- 변수 s를 선언하고, 기준 값 + start + end의 값이 target, 즉, 0과 가장 가까운 값이 되는지 탐색한다. 기록했던 값보다 0에 더 가깝다면 세 용액 x, y, z의 값을 갱신한다.
- s = target: 반복종료
- s < target: target과 가까워지려면 더 큰 값을 더해야하므로 start에 1을 더해서 탐색한다.
- s > target: target과 가까워지려면 더 작은 값을 더해야하므로 start에 1을 빼서 탐색한다.
- start가 end와 같아질 때까지 반복한다. (같으면 같은 용액임을 의미한다.)
🌷 풀이
n = int(input()) # 용액의 수
arr = sorted(list(map(int, input().split()))) # 각 용액의 특성값
min_s = 3000000001 # 0과 가장 가까운 값
x, y, z = 0, 0, 0
for i in range(n - 2):
start = i + 1
end = n - 1
while start < end: # start = end이면 같은 용액이 된다
s = arr[i] + arr[start] + arr[end]
if abs(s) < min_s:
min_s = abs(s)
x, y, z = arr[i], arr[start], arr[end]
if s < 0: # 0과 가까워지려면 좀 더 큰 값을 더해야 하므로 start + 1
start += 1
elif s > 0: # 0과 가까워지려면 좀 더 작은 값을 더해야 하므로 end - 1
end -= 1
else: # s == 0이라면 반복 종료
break
print(x, y, z)📚 Reference
'Etc > Algorithm' 카테고리의 다른 글
| [Algorithm] 분할 정복(Divide & Conquer) | 백준 2630번: 색종이 만들기 (0) | 2023.01.25 |
|---|---|
| [Python] 프로그래머스: 여행경로 (0) | 2023.01.05 |
| [Python] 백준 7569번: 토마토 (0) | 2023.01.04 |
| [Python] 백준 1260번: DFS와 BFS (0) | 2023.01.03 |
| [Java] 백준 1012번: 유기농 배추 (0) | 2022.11.21 |




댓글