이 글은 동빈나 님의 실전 알고리즘 강좌를 들으며 정리한 글입니다.
선택 정렬
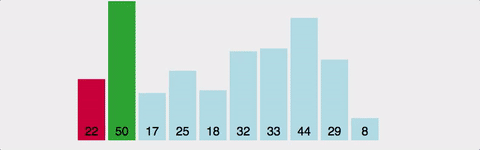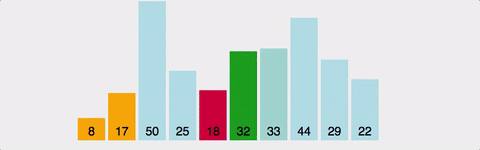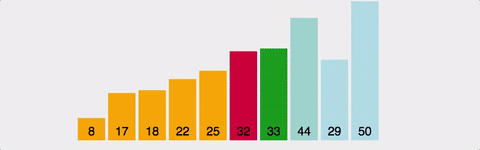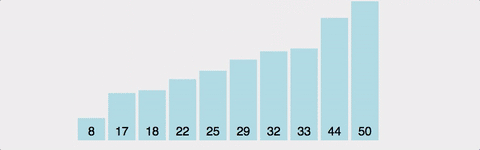
아무렇게나 놓인 데이터 중 가장 작은 데이터의 위치를 가장 앞에 있는 데이터 위치와 바꾼다. 이미 원소를 넣을 자리는 선택되어 있고 이 자리에 놓일 데이터를 찾는다.
- 정렬되지 않은 데이터 중 최솟값을 찾는다.
- 이 최솟값과 첫 번째 자리에 있는 데이터의 위치를 서로 바꾼다.
- 위 작업을 계속 반복한다.
시간 복잡도
O(n²)
반복 10 + 9 + 8 + ... + 1 : 등차수열10 * (10 + 1) / 2 = 55
→ N * (N + 1) / 2 : 컴퓨터에서 N에 엄청 큰 수라는 가정 하에 나누거나 더하는 연산은 의미가 없다
→ N * N
비효율적인 알고리즘 중 하나이다
void selectionSort(int[] arr) {
int min, temp;
for (int i = 0; i < arr.length - 1; i++) { // 마지막 원소는 정렬할 필요가 없다
min = i;
for (int j = i + 1; j < arr.length; j++)
if (arr[j] < arr[min]) // 지정 자리의 수보다 작은 값을 찾으면 자리를 바꾼다
min = j;
temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
System.out.println(Arrays.toString(arr));
}
버블 정렬

옆에 있는 값과 비교해서 더 적은 값을 앞으로 보낸다. 1회전이 완료될 때마다 우측에 정렬된 수가 쌓인다.
- 첫 번째 값과 두 번째 값을 비교해서 앞으로 보내고, 두 번째 값과 세 번째 값과 비교해서 정렬하는 것을 반복한다.
- 전체 한 번의 반복이 끝나게 되면 가장 큰 수가 우측에 위치하게 된다.
- 다음 전체 반복에서는 가장 우측에 있는 숫자를 제외하여 반복하도록 한다.
시간 복잡도
O(n²)
자리를 바꾸는 코드가 계속 반복되어서 선택 정렬과 시간 복잡도는 같지만 더 느리다. 가장 비효율적인 알고리즘이다.
void bubbleSort(int[] arr) {
int temp = 0;
for(int i = 0; i < arr.length; i++) {
for(int j = 1; j < arr.length - i; j++) {
if(arr[j-1] > arr[j]) {
temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
삽입 정렬

이미 정렬된 앞의 숫자들을 보고 적절한 위치를 찾는다.
_ 1 _ 10 _ 에서 5가 들어갈 위치: 1과 10은 정렬되어 있어서 10이랑만 위치를 바꾸면 된다.

시간 복잡도
O(n²)
선택, 버블 정렬과 복잡도는 같지만 연산이 가장 적게 일어나기 때문에 두 알고리즘보다 효율적이다. 거의 정렬된 상태일 수록 효율적인 알고리즘이다.
void insertionSort(int[] arr) {
for(int i = 1 ; i < arr.length ; i++){
int temp = arr[i];
int pre = i - 1;
while((pre >= 0) && (arr[pre] > temp)) { // 이전 인덱스가 더 큰 수일 때
arr[pre + 1] = arr[pre];
pre--;
}
arr[pre + 1] = temp;
}
System.out.println(Arrays.toString(arr));
}
퀵 정렬
대표적인 분할 정복 알고리즘이다
특정한 값을 기준으로 큰 숫자와 작은 숫자를 나눈다 → 피벗(Pivot): 기준값
- 가장 앞에 있는 숫자를 피벗값으로 설정한다. → 3, 5, 7, 1, 2
- 왼쪽(5)부터는 3보다 큰 숫자를, 오른쪽(2)부터는 3보다 작은 숫자를 찾는다. → 3, 5, 7, 1, 2
- 큰 값과 작은 값의 순서를 서로 바꾼다. → 3, 2, 7, 1, 5
- 계속 반복한다. → 3, 2, 7, 1, 5 → 3, 2, 1, 7, 5
- 큰 값과 작은 값이 엇갈리는 상황이 발생한다. → 3, 2, 1, 7, 5
- 작은 값과 피벗값을 바꿔 준다. → 1, 2, 3, 7, 5
- 3을 기준으로 왼쪽은 값이 작고, 오른쪽은 값이 크다.
- 왼쪽 집합과 오른쪽 집합을 나누어 피벗값을 설정하고 정렬을 반복한다. → 1, 2, 3, 7, 5
- 1, 2, 3, 7, 5 → 1, 2, 3, 7, 5 → 1, 2, 3, 7, 5 → 1, 2, 3, 5, 7
시간 복잡도
평균 O(N * logN)
최악 O(N²)
1 2 3 4 5 → 5 * 5 = 25
6 7 8 9 10 → 5 * 5 = 25
코드를 깔끔하게 만들기 위하여 재귀함수를 이용한다
public class Main {
private static int number = 10;
private static int[] data = {1, 10, 6, 2, 9, 3, 7, 4, 5, 8};
public static void quickSort(int[] data, int start, int end) {
if (start >= end) { //원소가 1개일 때
return;
}
int pivot = start; //pivot은 첫 번째 원소
int i = start + 1;
int j = end;
int temp;
while (i <= j) { //엇갈릴 때까지 반복
while (i <= end && data[i] < data[pivot]) { //pivot 값보다 큰 값을 만날 때까지
i++;
}
while (j > start && data[j] >= data[pivot]) { //pivot 값보다 작은 값을 만날 때까지
j--;
}
if (i > j) { //현재 엇갈린 상태면 pivot 값과 교체
temp = data[j];
data[j] = data[pivot];
data[pivot] = temp;
} else { //pivot 값보다 큰 값과 작은 값을 찾았고, 엇갈리지 않았다면 서로 교체
temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
//재귀 함수
quickSort(data, start, j - 1); //pivot 값과 j 위치의 값을 서로 바꿨으므로
quickSort(data, j + 1, end);
}
public static void main(String[] args) {
quickSort(data, 0, number - 1);
for(int i = 0; i < 10; i++) {
System.out.printf("%d ", data[i]);
}
}
}
병합 정렬
'분할 정복' 방법을 채택한 알고리즘
피벗 값에 따라 편향되게 분할될 가능성 있었던 퀵 정렬과는 다르게
정확히 반을 나누기 때문에 시간 복잡도를 유지한다
일단 반으로 나누고 나중에 합쳐서 정렬한다!

너비가 8일 때 높이가 3이다 → log₂8 = 3 → 단계가 커질수록 2¹ 2² 2³ 처리 가능한 데이터가 아주 많아짐
이미 정렬된 데이터를 활용하므로 N을 보장한다
시간 복잡도
O(N * logN)
📚 Reference
'Etc > Algorithm' 카테고리의 다른 글
| [JAVA] 백준 2751번: 수 정렬하기 2 (0) | 2022.06.27 |
|---|---|
| [JAVA] 백준 2752번: 세수정렬 (0) | 2022.06.26 |
| [JAVA] 백준 17478번: 재귀함수가 뭔가요? (0) | 2022.06.24 |
| [JAVA] 백준 11720번: 숫자의 합 (0) | 2022.05.28 |
| [JAVA] 백준 11654번: 아스키 코드 (0) | 2022.05.28 |




댓글